
- FEM GLOBAL SOURCE VECTOR 2D SOFTWARE
- FEM GLOBAL SOURCE VECTOR 2D CODE
- FEM GLOBAL SOURCE VECTOR 2D SERIES
This causes almost no additional computational cost. First, to generate a roughly homogeneously fine mesh discretisation around all receiver sites, our new error estimator weights the adjoint source term by the approximate decay of the electric field with increasing distance from the primal source using the expression for a homogeneous half-space. To formulate an improved error estimator suitable for controlled-source electromagnetic problems, we developed literature approaches of mesh refinement further targeting three aspects.
FEM GLOBAL SOURCE VECTOR 2D CODE
Our modelling code aims at finding a good compromise between the necessary solution accuracy at the points of interest and the general problem size by using a goal-oriented mesh refinement strategy designed for models of variable electric conductivity and magnetic permeability.

FEM GLOBAL SOURCE VECTOR 2D SOFTWARE
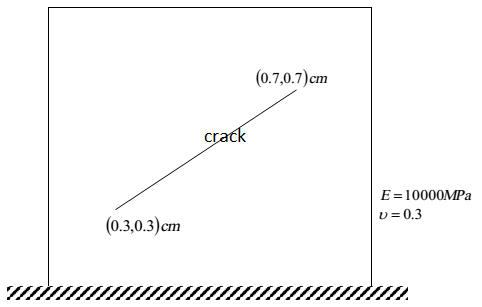
To evaluate electromagnetic data acquired across complex subsurface structures, software performing accurate 3D modelling is required, especially for incorporation in inversion approaches. We developed a three-dimensional (3D) forward modelling code, which simulates controlled-source electromagnetic problems in frequency domain using edge-based finite elements and a total electric field approach. Therefore, the natural spaces of the fields are $[\mathit$ and the correlation to the classical Cauchy continuum theory. The corresponding elastic energy functional contains the gradient of the displacement field, the microdistortion field and its Curl (the micro-dislocation). The theory introduces a microdistortion field, encompassing nine extra degrees of freedom for each material point. The relaxed micromorphic continuum offers an alternative method by instead enriching the kinematics of the mathematical model. In terms of finite element computations, this can be done by modelling the entire body, including every interior cell. As a result, the classical continuum theory cannot capture their mechanical behaviour without fully resolving the underlying microstructure. However, many materials, such as porous media or metamaterials, exhibit a pronounced microstructure. The classical Cauchy continuum theory is suitable to model highly homogeneous materials. Numerical experiments are presented to demonstrate the robustness and effectiveness of the proposed preconditioners within both Krylov subspace and Chebyshev accelerations compared with some already available preconditioned Krylov subspace methods. Such results ensure efficient Krylov subspace acceleration methods and a parameter-free Chebyshev acceleration method, which are both robust in view of all discretization and model parameters. Problem independent eigenvalue bounds and upper bound approximations of the condition numbers of the eigenvector matrices are obtained for the preconditioned matrices. Parameter robust preconditioners are proposed for solving these linear systems along with information on practical algorithm implementation and detailed spectral analysis.
FEM GLOBAL SOURCE VECTOR 2D SERIES
By using the multiharmonic FEM, the linear algebraic equations characterizing the first-order optimality conditions can be decoupled into a series of parallel solvable block 4 × 4 linear systems with respect to the cosine and sine Fourier coefficients of the state and scaled control variables for different frequencies. We are concerned with efficient solutions of the time-periodic parabolic optimal control problems.


 0 kommentar(er)
0 kommentar(er)
